Termodinamica

Sistema termodinamico

#

La termodinamica è la scienza che studia le trasformazioni di energia e il loro legame con il calore¹ e il lavoro² che un sistema³ scambia con l’ambiente⁴.

Un sistema termodinamico è una porzione ben definita di materia o spazio che viene isolata e studiata, separata dall’ambiente esterno tramite un confine (reale o immaginario).

📝 In breve: In termodinamica scegliamo una parte di spazio e la racchiudiamo con un confine. Può essere:

• reale -> es. una pentola
• immaginario -> es. un volume d’aria in una stanza
• energia (calore, lavoro)
• materia (entrate o uscite di sostanza)

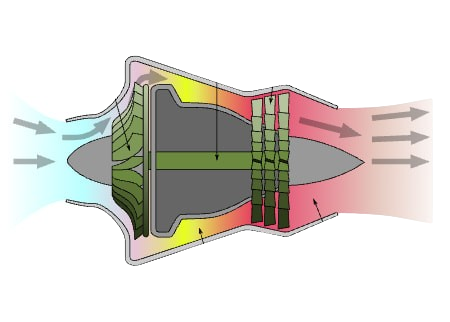
Quando un sistema scambia solo energia con l’ambiente⁴, ma non materia, si chiama sistema chiuso. Se invece ci sono scambi di materia (entrate o uscite), allora si parla di sistema aperto.

• Sistema chiuso (massa costante): scambia solo energia, non materia.
  es. serbatoio ermetico⁵ che scambia calore.
• Sistema aperto (massa variabile): scambia energia e materia.
  es. turbina a gas (aria entra ed esce).

Variabili di stato

#

Lo stato di un sistema termodinamico contenente un gas può essere descritto completamente conoscendo tre grandezze fisiche fondamentali, dette variabili di stato⁶:

• \(p\): pressione assoluta
• \(T\) temperatura assoluta
• \(v\) il volume specifico

Il volume specifico invece rappresenta il volume \(V\) occupato da una certa quantità di sostanza, rapportato al numero di moli \(n\). Si definisce con la relazione:

$$ v = \frac{V}{n} [m^3/mol] $$

dove:

• \(V\) è il numero geometrico occupato dal gas
• \(n\) è il numero di moli della sostanza

Gas ideali

#

Studiare in modo completo un sistema termodinamico a fluido sarebbe molto complicato se si considerassero tutte le caratteristiche reali dei gas.

Per semplificare si utilizza il modello del gas ideale⁷ (o gas perfetto): un modello teorico che, grazie ad alcune ipotesi, permette di descrivere il comportamento dei gas in maniera abbastanza precisa e in accordo con i dati sperimentali.

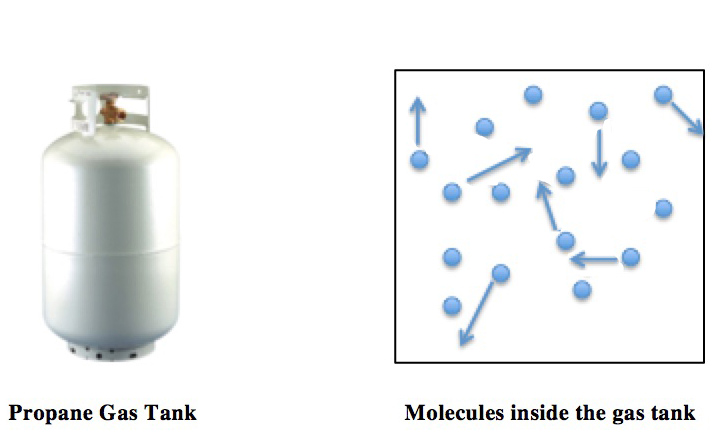
Nel gas ideale⁷ si ipotizza che:

• le molecole siano tutte uguali, di forma sferica e con un volume proprio trascurabile rispetto a quello del recipiente
• non ci siano forze di interazione a distanza tra le molecole
• gli urti tra molecole e con le pareti siano perfettamente elastici, cioè senza perdita di energia cinetica
• non ci sono attriti

Un gas reale può essere considerato ideale quando si trova lontano dalle condizioni di liquefazione, quindi a pressioni relativamente basse e temperature piuttosto alte. La maggior parte dei gas usati nelle macchine a fluido può essere trattata come ideale con un errore molto piccolo (circa 0,1%).

Fa eccezione il vapore acqueo: nelle applicazioni come le turbine a vapore lavora vicino alla condensazione, quindi non rispetta le legi dei gas ideali e richiede modelli più complessi.

📝 In breve:

• Il gas ideale⁷ è un modello che serve a semplificare lo studio dei gas.
• Si finge che le molecole siano puntini senza volume, che non abbiamo forze tra loro, che rimbalzino perfettamente quando urtano e che non ci siano attriti.
• Questa finzione funziona bene per molti gas quando sono lontani dal diventare liquidi, cioè a bassa pressione e alta temperatura.
• Non vale invece per il vapore acqueo, che spesso si trova vicino alla condensazione e quindi non si comporta come un gas ideale.

Equazione di stato dei gas ideali

#

In un gas ideale⁷, le tre variabili di stato⁶: pressione \(p\), volume specifico \(v\) e temperatura \(T\) sono collegate da una relazione chiamata equazione di stato:

$$ p \cdot v = R \cdot T $$

Dove:

• \(p\) = pressione assoluta (\(Pa\))
• \(v\) = volume specifico (\(m^3/mol\))
• \(T\) = temperatura assoluta (\(K\))
• \(R\) = costante dei gas ideali = 8,314 \((J/(mol \cdot K\))

Con questa equazione, conoscendo due variabili di stato è possibile determinare la terza in modo univoco. La relazione si basa su tre leggi sperimentali fondamentali:

• La legge di Boyle-Mariotte: a temperatura costante, pressione e volume sono inversamente proporzionali (se la pressione aumenta, il volume diminuisce).

• La prima legge di Gay-Lussac: a pressione costante, il volume cresce proporzionalmente alla temperatura.

• La seconda legge di Gay-Lussac: a volume costante, la pressione cresce proporzionalmente alla temperatura.

Legge	Variabile costante	Relazione tra le altre
Boyle-Mariotte	Temperatura (T)	\(p \cdot v = \text{cost}\) → \(p\) e \(v\) inversi
1ª legge di Gay-Lussac	Pressione (p)	\(v \propto T\)
2ª legge di Gay-Lussac	Volume (v)	\(p \propto T\)

📝 In breve

Un gas ideale si comporta come una sostanza “perfetta” dove:

• Le molecole occupano pochissimo spazio
• Non interagiscono tra loro a distanza
• Gli urti tra molecole e pareti sono elastici
• Non c’è attrito

Con queste ipotesi, possiamo usare l’equazione \(p \cdot v = R \cdot T\) per capire come cambia pressione, volume e temperatura durante le trasformazioni del gas.

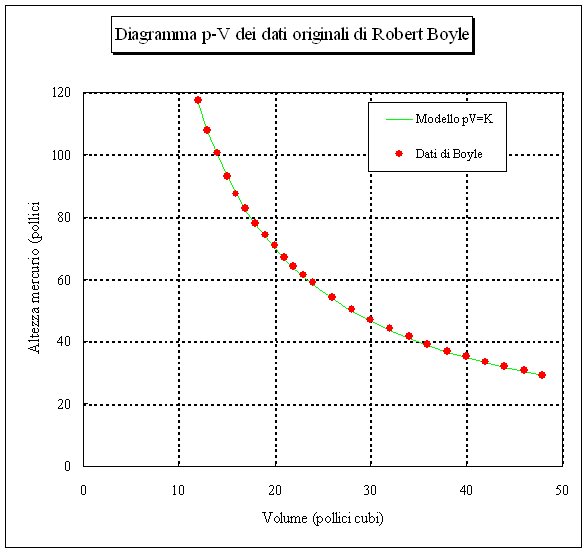
Legge di Boyle-Mariotte

#

La legge di Boyle-Mariotte, enunciata nel 1662 da Robert Boyle e perfezionata nel 1676 da Edme Mariotte, descrive il comportamento di un sistema termodinamico in cui il volume e la pressione vengono fatti variare mantenendo la temperatura costante (trasformazione isoterma).

Con queste condizioni vale la relazione:

$$ p \cdot v = costante $$

dove:

• \(p\) = pressione del gas
• \(v\) = volume specifico del gas

Cosa significa in pratica:

Se la pressione aumenta, il volume diminuisce proporzionalmente, e viceversa. Ad esempio:

• Se la pressione raddoppia -> il volume si dimezza
• Se la pressione si dimezza -> il volume raddoppia

In altre parole, pressione e volume sono inversamente proporzionali durante una trasformazione isoterma.

Prima Legge di Gay-Lussac

#

La prima legge di Gay-Lussac afferma che in una trasformazione isobara (cioè a pressione costante), il volume specifico \(v\) di un gas ideale varia linearmente con la temperatura \(t\) espressa in \(\text{\textdegree C}\) secondo l’equazione:

$$ v = v_0 \cdot (1 + \alpha \cdot t) $$

dove:

• \(v_0\) = volume a \(t = 0 \text{\textdegree C}\)
• \(\alpha\) = coefficiente di espansione dei gas (per i gas ideali vale sempre: \(\alpha = \frac{1}{273,15} \text{\textdegree}{C^{-1}}\)

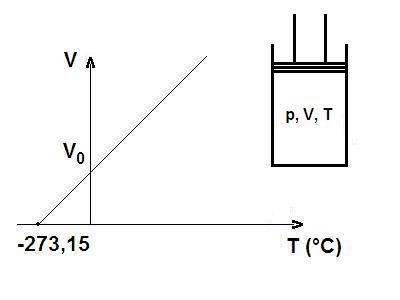
Analizzando il grafico della legge, si vede che il volume del gas tende a diventare nullo a:

$$ t = -273,15\,^{\circ}\text{C}. $$

Questo valore è uguale allo zero assoluto, scelto come limite inferiore delle temperatura: al di sotto di esso, la legge non avrebbe più senso fisico, perchè implicherebbe un volume negativo, cosa impossibile.

📝 In breve:

Se un gas è mantenuto a pressione costante, il suo volume aumenta o diminuisce in proporzione alla temperatura.

• Quando la temperatura cresce, anche il volume cresce.
• Quando la temperatura scende, il volume diminuisce.
• Arrivando a \(-273,15\,^{\circ}\text{C}\), il gas si ridurebbe a volume zero: questo è il motivo per cui questa temperatura è il punto di partenza della scala Kelvin (0 K).

Seconda Legge di Gay-Lussac

#

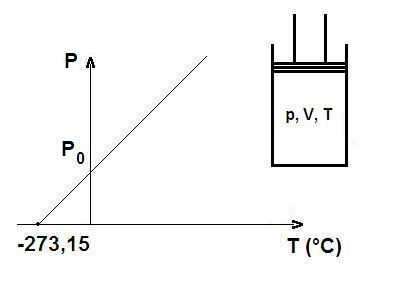
La seconda legge di Gay-Lussac afferma che in una trasformazione isocora, cioè a volume costante, la pressione \(p\) di un gas varia linearmente con la temperatura \(t\) espressa in \(^{\circ}\text{C}\), secondo l’equazione:

$$ p = p_0 \cdot (1 + \alpha \cdot t) $$

dove:

• \(p_0\) = pressione del gas a \(t = 0\, ^{\circ}\text{C}\)
• \(\alpha\) = coefficiente di espansione dei gas

In parole semplici

• Se il volume non cambia, aumentando la temperatura aumenta anche la pressione.
• La legge mostra un’ulteriore conferma dello zero assoluto: infatti, per valori di temperatura inferiori a \(-273,15\, ^{\circ}\text{C}\), la pressione risulterebbe negativa, cosa impossibile nella realtà.

Principi della termodinamica

#

Lo studio dei sistemi termodinamici si basa su alcuni principi fondamentali, enunciati nel XIX secolo, che stabiliscono come e con quali limiti avvengono le trasformazioni energetiche.

Per la termodinamica applicata ai processi industriali sono essenziali in particolare:

• il Primo principio, che riguarda la conservazione dell’energia
• il Secondo principio, che introduce un limite all’uso dell’energia e definisce la direzione spontanea dei processi.

Primo principio

#

Il primo principio della termodinamica è la traduzione in ambito tecnico-scientifico del più generale principio di conservazione dell’energia. Serve per fare il bilancio energetico di un sistema che può scambiare con l’ambiente calore (\(Q\)) e lavoro (\(L\)).

In altre parole:

“La variazione dell’energia interna di un sistema termodinamico chiuso è uguale alla differenza tra il calore fornito al sistema e il lavoro compiuto dal sistema sull’ambiente.”

Matematicamente si scrive:

$$ \Delta U = Q - L $$

dove:

• \(U\) = energia interna del sistema
• \(Q\) = calore scambiato (positivo se ricevuto dal sistema)
• \(L\) = lavoro scambiato (positivo se compiuto dal sistema)

Nota bene: questa convenzione dei segni è fondamentale. Se il sistema riceve calore, l’energia interna aumenta; se compie lavoro sull’ambiente, la sua energia interna diminuisce.

Secondo principio

#

Per il primo principio in un sistema termodinamico è possibile trasformare il calore in lavoro, operazione che si realizza praticamente grazie alle macchine termiche.

Il secondo principio introduce però una limitazione: non tutta la quantità di calore \(Q\) assorbita può essere trasformata in lavoro \(L\).

Secondo l’enunciato di Lord Kelvin (1824-1907):

“E’ impossibile realizzare una trasformazione ciclica il cui unico risultato sia la trasformazione in lavoro di tutto il calore assorbito da una sola sorgente”.

Da questo deriva che:

“E’ impossibile realizzare una macchina termica il cui rendimento sia pari al 100%”

In altre parole, in una macchina termica a ciclo chiuso, dove lo stato finale del gas coincide con quello iniziale, non è possibile trasformare completamente il calore \(Q\) in lavoro \(L\).

A livello pratico, questo significa che per funzionare una macchina termica deve avere:

• una sorgente calda (alta temperatura) da cui preleva calore;
• una sorgente fredda (temperatura più bassa) dove viene ceduta la parte di calore che non può essere convertita in lavoro.

Trasformazioni termodinamiche fondamentali

#

Una trasformazione termodinamica è un processo che modifica lo stato di un sistema attraverso uno scambio di calore e/o lavoro con l’ambiente, variando così pressione, temperatura e volume specifico.

Una trasformazione è detta reversibile se può avvenire nei due sensi (andata e ritorno) senza perdite di energia.

Nella realtà, però, tutte le trasformazioni sono irreversibili, perchè avvengono con perdite dovute ad attriti, urti molecolari e resistenze interne. Per semplificare lo studio dei sistemi, si considera in teoria che le trasformazioni siano reersibili, così da poterle descrivere con modelli matematici più semplici.

In questa visione ideale, il sistema passa dallo stato iniziale a quello finale attraverso molti stati di equilibrio intermedi, formando un percorso continuo.

Le quattro trasformazioni fondamentali sono:

• Isobara -> a pressione costante
• Isocora -> a volume costante
• Isoterma -> a temperatura costante
• Adiabatica -> senza scambio di calore

Sul piano di Clapeyron (grafico con volume specifico v sull’asse orizzontale e pressione p su quello verticale), ogni trasformazione è rappresentata da una linea continua con una propria equazione caratteristica. Nei paragrafi successivi, queste trasformazioni vengono analizzate e disegnate su tale piano.

📝 Spiegazione: Le trasformazioni termodinamiche descrivono come cambia un gas quando riceve o cede calore o lavoro.

Quelle reversibili sono ideali e senza perdite, mentre quelle irreversibili sono reali e con sprechi di energia.
I principali tipi di trasformazione sono quattro: isobara (pressione fissa), isocora (volume fisso), isoterma (temperatura costante) e adiabatica (nessuno scambio di calore).
Nel grafico p-v, ognuna di queste trasformazioni ha una curva o una retta che mostra come variano le grandezze del sistema.

Trasformazione isobara

#

Una trasformazione isobara è una trasformazione termodinamica che avviene a pressione costante. Un modo semplice per realizzarla è riscaldare un gas all’interno di un cilindro chiuso con un pistone mobile, sul quale è posto un peso fisso. Quando la temperatura del gas aumenta, il pistone si solleva, ma la pressione resta invariata.

L’equazione che descrive l’isobara nel piano di Clapeyron è:

$$ p = \text{costante} $$

e corrisponde graficamente a una linea orizzontale.

Il calore assorbito dal gas si calcola con la legge fondamentale della termologia:

$$ Q = m \cdot c_s \cdot \Delta T $$

Se si considera una massa unitaria di gas (cioè $m = 1$), la formula diventa:

$$ Q = c_p \cdot \Delta T [J/mol] $$

dove:

• $c_p$ è il calore specifico a pressione costante (espresso in $J/(mol \cdot K))
• $\Delta T$ è la variazione di temperatura in kelvin

Durante l’espansione da $v_1$ a $v_2$ il pistone compie un lavoro. Nel piano di Clapeyron, questo lavoro corrisponde all’area sotto la linea isobara, che ha forma rettangolare

Perciò:

$$ L = p_1 \cdot (v_2 - v_1) [J/mol] $$

dove:

• $p_1$ è la pressione costante (in pascal)
• ($v_2$ - $v_1$) è la variazione di volume specifico (in $m^3/mol$).

📝 Spiegazione: Isobara significa pressione costante (“iso” vuol dire uguale, “bara” vuol dire pressione). Se scaldi un gas sotto un pistone, il gas si espande e solleva il pistone, ma la pressione resta uguale. In questo processo, il gas assorbe calore (Q) e lo trasforma in lavoro (L), spingendo il pistone verso l’alto. Nel grafico pressione-volume, la trasformazione è rappresentata da una linea orizzontale.

Trasformazione isocora

#

Si definisce isocora una trasformazione termodinamica che avviene a volume costante. Il metodo sperimentale più semplice per realizzarla consiste nel fornire calore a un gas contenuto in un cilindro chiuso da un pistone bloccato, in modo che il volume non possa variare.

L’equazione che descrive l’isocora nel piano di Clapeyron è

$$ v = \text{costante} $$

che corrisponde graficamente a una retta verticale.

Il calore ricevuto, riferito a una massa unitaria di gas (m = 1 mol), si calcola mediante la legge fondamentale della termologia:

$$ Q = c_v \cdot \Delta T [J/mol] $$

dove:

• $c_0$ è il calore specifico a volume costante espresso in J / (mol \cdot K)
• $\Delta T$ rappresenta la variazione di temperatura in Kelvin.

Osservando il piano di Clapeyron, si nota che la trasformazione isocora non sottende alcuna area, quindi il gas non compie lavoro meccanico:

$$ L = 0 $$

Questo è coerente con la definizione meccanica di lavoro, essendo il pistone fermo e quindi privo di spostamento.

Applicando il primo principio della termodinamica:

$$ \Delta U = Q - L $$

e sostituendo $L = 0$, si ottiene:

$$ \Delta U = Q $$

Ne consegue che tutto il calore assorbito dal sistema si trasforma interamente in variazione di energia interna del gas.

📝 Spiegazione: In una trasformazione isocora, il volume non cambia, quindi non si compie alcun lavoro. Quando forniamo calore al gas, questo aumenta solo la sua energia interna, cioè la temperatura. In pratica:

• il pistone resta fermo, quindi $L = 0$
• tutto il calore fornito serve ad aumentare l’energia del gas.

Trasformazione isoterma

#

Si definisce isoterma una trasformazione termodinamica che avviene a temperatura costante. In linea di principio, si può ottenere una trasformazione isoterma attraverso una compressione o una dilatazione molto lenta, che consenta al sistema di mantenersi sempre alla stessa temperatura di equilibrio. Tuttavia, a livello pratico, questa condizione non è facilmente realizzabile perché non compatibile con il normale funzionamento di una macchina termica.

L’equazione che descrive l’isoterma nel piano di Clapeyron è

$$ p \cdot v = \text{costante} $$

che rappresenta graficamente un’iperbole equilatera. Questo significa che, a temperatura costante, se il volume aumenta la pressione diminuisce, e viceversa, in modo proporzionale.

Il lavoro compiuto lungo la trasformazione che va dallo stato 1 allo stato 2 corrisponde graficamente all’area sottesa alla curva. Per calcolarlo si usa la formula:

$$ L = p_1 \cdot v_1 \cdot ln(\frac{v_2}{v_1}) = p_1 \cdot v_1 \cdot ln(\frac{p_1}{p_2}) [J/mol] $$

dove “ln” indica il logaritmo naturale. Poichè la temperatura rimane costante, si ha:

$$ \Delta U = 0 $$

e quindi, in base al primo principio della termodinamica,

$$ Q = L $$

📝 Spiegazione:
In una trasformazione isoterma, il lavoro compiuto dal gas si trasforma interamente in calore (e viceversa).
Se il gas si espande, assorbe calore dall’esterno e lo converte in lavoro; se invece si comprime, cede calore e riceve lavoro.
Questo tipo di trasformazione è alla base di molti processi termodinamici ideali, come nel ciclo di Carnot.

Trasformazione adiabatica

#

Si definisce adiabatica una trasformazione termodinamica in cui il fluido non cede né acquista calore. Sperimentalmente, si può realizzare un’adiabatica attraverso una compressione o una dilatazione estremamente rapida, durante la quale, proprio per via della breve durata, non vi sia tempo sufficiente per un significativo scambio di calore tra sistema e ambiente. Sotto questa ipotesi si può considerare Q=0 Q=0.

L’equazione che descrive l’adiabatica nel piano di Clapeyron è:

$$ p : v^k = \text{costante} $$

in cui $k$ rappresenta il coefficiente di dilatazione adiabatica, definito come rapporto tra calore specifico a pressione costante e a volume costante:

$$ k = \frac{c_p}{c_v} $$

Per l’aria, che rappresenta il gas di riferimento per lo studio dei cicli termodinamici, $k=1,4$. Graficamente, la curva di una trasformazione adiabatica è simile a quella di un’isoterma ma con un andamento molto più ripido.

Il calcolo del lavoro L di una compressione o espansione adiabatica non è di immediata esecuzione. La formulazione più semplice risulta:

$$ L = -c_v \cdot \Delta T [J/mol] $$

in cui $c_v$ è il calore specifico a volume costante e $\Delta T$ è la variazione di temperatura del fluido. Sapendo che in una trasformazione adiabatica $Q = 0$, dal primo principio si ottiene:

$$ \Delta U = -L $$

Da questa relazione si deduce che:

• durante una compressione adiabatica, il sistema acquista lavoro dall’esterno (con L quindi negativo), l’energia interna U aumenta e quindi il gas si scalda;
• durante un’espansione adiabatica, il sistema compie un lavoro (con L quindi positivo), l’energia interna U diminuisce e quindi il gas si raffredda.

Queste osservazioni sono di fondamentale importanza perché suggeriscono, ad esempio, il modo per innescare la combustione spontanea all’interno di un motore, semplicemente attraverso una compressione che porti la temperatura oltre quella di accensione del combustibile.

📝 Spiegazione: Una trasformazione adiabatica avviene senza scambio di calore con l’esterno (Q = 0). Il lavoro compiuto o ricevuto modifica direttamente l’energia interna del gas, causando variazioni di temperatura: si scalda se compresso, si raffredda se si espande.

Cicli termodinamici

#

Un ciclo termodinamico è una serie di trasformazioni durante le quali un fluido, come un gas, ritorna alle sue condizioni iniziali di pressione, temperatura e volume. In pratica, il sistema compie un percorso chiuso: parte da uno stato, cambia più volte (per esempio si comprime, si espande, si scalda, si raffredda) e alla fine torna allo stato di partenza.

Di solito questi cicli sono studi teorici, perchè si basano su un gas perfetto racchiuso in un sistema chiuso e isolato, cioè senza scambi di materia o calore con l’esterno. Anche se ideali, sono molto utili per capire come funzionano davvero i cicli industriali (come quelli dei motori), perchè le stesse leggi si applicano anche nella realtà, con qualche correzzione.

I principali cicli termodinamici fondamentali utilizzati nello studio delle macchine termiche (come motori e turbine) sono quattro:

• Ciclo di Carnot
• Ciclo Otto - Beau de Rochas
• Ciclo Diesel
• Ciclo Sabathé

📝 Spiegazione:
Un ciclo termodinamico è un processo dove un gas torna al punto di partenza dopo varie trasformazioni. Serve per produrre lavoro meccanico (come nei motori). Anche se nella realtà non esistono cicli perfetti, studiarli aiuta a capire come migliorare il rendimento dei motori. I cicli più famosi (Carnot, Otto, Diesel e Sabathé) rappresentano i modelli base da cui derivano tutti i motori termici moderni.

Ciclo di Carnot

#

Il ciclo di Carnot descrive il funzionamento ideale di una macchina termica, cioè un dispositivo che trasforma calore in lavoro.
Secondo il secondo principio della termodinamica, non è possibile trasformare tutto il calore proveniente da una sola sorgente in lavoro meccanico.
Serve quindi una sorgente calda (a temperatura \( T_1 \)) e una sorgente fredda (a temperatura \( T_2 \)) dove scaricare parte del calore.

Nel 1824 il fisico francese Sadi Carnot definì un ciclo formato da quattro trasformazioni reversibili, che rappresenta il modello ideale con il massimo rendimento teorico possibile.

Le quattro fasi

#

1. Espansione isoterma (1–2)
   Il fluido assorbe una quantità di calore \( Q_1 \) dalla sorgente calda a temperatura costante \( T_1 \), e si espande compiendo lavoro.

2. Espansione adiabatica (2–3)
   Il fluido continua ad espandersi senza scambio di calore (\( Q = 0 \)), raffreddandosi fino a \( T_2 \).

3. Compressione isoterma (3–4)
   Il fluido viene compresso a temperatura costante \( T_2 \), cedendo calore \( Q_2 \) alla sorgente fredda.

4. Compressione adiabatica (4–1)
   Il fluido viene compresso rapidamente senza scambio di calore, tornando alla temperatura iniziale \( T_1 \) e chiudendo il ciclo.

Calcolo del rendimento

#

Il rendimento di una macchina termica misura quanta parte del calore assorbito viene trasformata in lavoro:

\[ \eta = \frac{L}{Q_1} \]

Dalla prima legge della termodinamica:

\[ \Delta U = Q - L \]

Poiché in un ciclo completo l’energia interna non cambia (\( \Delta U = 0 \)):

\[ L = Q_1 - Q_2 \]

Sostituendo nella formula del rendimento:

\[ \eta = \frac{Q_1 - Q_2}{Q_1} = 1 - \frac{Q_2}{Q_1} \]

Per il ciclo di Carnot vale anche che le quantità di calore sono proporzionali alle temperature delle sorgenti:

\[ \frac{Q_1}{Q_2} = \frac{T_1}{T_2} \]

Da cui deriva la formula più usata:

\[ \eta = 1 - \frac{T_2}{T_1} \]

Come aumentare il rendimento

#

• Se il rapporto \( \frac{T_2}{T_1} \) diminuisce, il rendimento aumenta.
• In teoria, se \( T_2 = 0 \) (zero assoluto), il rendimento sarebbe 100%.
  Ma questo è impossibile, quindi nessuna macchina reale può avere rendimento unitario.

Per migliorare l’efficienza si cerca di:

• aumentare la temperatura della sorgente calda \( T_1 \);
• ridurre il più possibile la temperatura della sorgente fredda \( T_2 \).

Nelle macchine reali, però, \( T_2 \) dipende spesso dalla temperatura dell’ambiente, quindi si può agire solo su \( T_1 \),
usando materiali che resistono a temperature elevate (come le superleghe al nichel nelle turbine a gas, che possono arrivare fino a 1300 °C).

📝 Spiegazione:

Il ciclo di Carnot è un modello teorico che mostra il modo più efficiente possibile per trasformare calore in lavoro.
Funziona con:

• una sorgente calda da cui prende calore;
• una sorgente fredda dove scarica il calore che non riesce a trasformare.

Il rendimento dipende solo dalle temperature:
più grande è la differenza tra caldo e freddo, più energia utile si ottiene.
Tuttavia, nessuna macchina reale potrà mai essere perfetta: un po’ di energia andrà sempre persa.

Ciclo Otto - Beau de Rochas

#

Il ciclo Otto - Beau de Rochas è il modello teorico di riferimento dei motori a benzina (motori ad accensione comandata). Il nome deriva da:

• Alphonse Beau de Rochas (1815-1893): che lo brevettò
• Nikolaus A. Otto (1832-1891): che lo realizzò per primo

Il ciclo è formato da quattro trasformazioni termodinamiche:

1. Compressione adiabatica (1-2) -> Il gas viene compresso senza scambio di calore.
2. Riscaldamento isocoro (2-3) -> A volume costante, il gas assorbe calore $Q_1$ dalla sorgente calda.
3. Espansione adiabatica* (3-4) -> Il gas si espande, compiendo lavoro e raffreddandosi.
4. Raffreddamento isocoro (4-1) -> A volume costante, il gas cede calore $Q_2$ alla sorgente fredda.

Poichè il ciclo è chiuso, la variazione di energia interna è nulla:

$$ \Delta U = 0 $$

quindi il lavoro utile è:

$$ L = Q_1 - Q_2 $$

e il rendimento termico è:

$$ \eta = 1 - \frac{Q_2}{Q_1} $$

Rapporto di compressione

#

Si definisce rapporto volumetrico di compressione il parametro:

$$ \epsilon = \frac{v_1}{v_2} $$

dove:

• $v_1$: volume del gas prima della compressione
• $v_2$: volume dopo la compressione

Il rendimento del ciclo Otto può essere espresso come:

$$ \eta = 1 - \frac{1}{\epsilon^{k - 1}} $$

dove:

• $k$: coefficiente di dilatazione adiabatica (per l’aria $k = 1,4$).

Da questa formula si capisce che aumentando il rapporto di compressione $\epsilon$, aumenta anche il rendimento. Tuttavia, nei motori a benzina non si può esagerare: se la compressione è troppo alta, la miscela aria-carburante detona in modo anomalo.

Per migliorare il rendimento, nei motori moderni si usa la sovralimentazione: un turbocompressiore aumenta la pressione dell’aria aspirata, permettendo maggiore potenza e minori consumi.

📝 In breve: Il ciclo Otto è quello dei motori a benzina: l’aria viene compressa, scaldata, espansa e poi raffreddata, tornando al punto di partenza.

• Più il gas è compresso -> più energia utile si ottiene. Ma se la compressione è troppo alta -> la benzia scoppia da sola (detonazione) Il trucco moderno è usare il turbo, che “spinge più l’aria” nel motore migliorando potenza e rendimento.

In breve: più compressione = più efficienza, ma solo fino a un certo limite.

Ciclo Diesel

#

Il ciclo Diesel è un ciclo termodinamico che descrive il funzionamento dei motori a gasolio (motori ad accensione spontanea), utilizzati sopratutto nei grandi motori industriali e navali. Prende il nome dall’ingegnere tedesco Rudolf Diesel (1858-1913), che lo ideò.

Il ciclo è formato da quattro trasformazioni termodinamiche:

1. **Compressione adiabatica (1-2) Il fluido viene compresso senza scambio di calore -> la temperatura aumenta.
2. **Espansione isobara (2-3) Il fluido assorbe calore $Q_1$ dalla sorgente calda a pressione costante -> avviene la combustione
3. **Espansione adiabatica (3-4) Il fluido si espande e compie lavoro -> la temperatura diminuisce
4. **Trasformazione isocora (4-1) Il fluido cede il calore residuo $Q_2$ alla sorgente fredda a volume costante, tornando alle condizioni iniziali.

Il ciclo Diesel dipende da due grandezze principali:

• Rapporto di compressione

$$ \epsilon = \frac{v_1}{v_2} $$

E’ analogo a quello del ciclo Otto: indica quanto il gas viene compresso.

• Rapporto volumetrico di combustione

$$ \beta = \frac{v_3}{v_2} $$

Indica quanto aumenta il volume durante la combustione (cioè durante la fase isobara).

Rendimento del ciclo Diesel

#

Il rendimento teorico (cioè l’efficienza con cui trasforma calore in lavoro) è dato da:

$$ \eta = 1 - \frac{1}{\epsilon^{(k-1)}} \cdot [\frac{\beta^k - 1}{k \cdot (\beta - 1)}] $$

dove:

• $k$ = coefficiente di dilatazione adiabatica (per l’aria $\tilde$ 1,4)
• $\epsilon$ = rapporto di compressione
• $\beta$ = rapporto di combustione

Poichè il termine tra parentesi quadre è maggiore di 1, a parità di rapporto di compressione, il ciclo Diesel ha rendimento inferiore al ciclo Otto. Tuttavia, nella pratica, i motori Diesel lavorando con rapporti di compressione molto più alti, e quindi sono più efficienti dei motori a benzina.

📝 In breve: Il motore Diesel funziona comprimendo l’aria fino a farla diventare estremamente calda, in quel momento viene iniettato il gasolio, che si accende da solo senza bisogno di una candela, grazie alla temperatura elevata. Durante la fase di combustione la pressione resta costante e il pistone viene spinto verso il basso, producendo lavoro meccanico. Anche se dal punto di vista teorico il rendimento del ciclo Diesel è leggermente inferiore a quello del ciclo Otto, nella realtà i motori Diesel risultano più efficienti, perchè comprimono molto di più l’aria. Per questo motivo sono largamente impiegati in camion, treni e navi, dove servono potenza, efficienza e consumi ridotti.

Ciclo Sabathè

#

Il ciclo Sabathè è un ciclo termodinamico che rappresenta un compromesso tra il ciclo Otto (motori a benzina) e il ciclo Diesel (motori a gasolio). Viene utilizzato per descrivere in modo più realistico il funzionamento dei motori di media o piccola potenza, dove nè il modello Otto nè quello Diesel riescono a rappresentare perfettamente la realtà.

Durante la fase in cui il fluido assorbe calore (fase 2-3), nel ciclo Sabathè questo avviene in due momenti distinti:

• una fase isocora (a volume costante), simile a quella del ciclo Otto
• una fase isobara (a pressione costante), come nel ciclo Diesel

Il ciclo Sabathè è quindi formato da cinque trasformazioni termodinamiche:

1. una compressione adiabatica (1-2)
2. una trasformazione isocora con assorbimenti di una prima parte di calore $Q’_1$ dalla sorgente calda (2-2')
3. una trasformazione isobara con assorbimento di una seconda parte di calore $Q"_1$ dalla sorgente calda (2’-3)
4. una espansione adiabatica (3-4)
5. una trasformazione isocora con cessione del calore residuo $Q_2$ alla sorgente fredda (4-1)

Come per gli altri cicli, anche per il Sabathè si può ricavare una formula matematica per il rendimento, ma di solito è più chiaro confrontare graficamente il rendimento dei vari cicli in funzione del rapporto di compressione $\epsilon$.

Per un valore tipico di $\epsilon = 10$, il rendimento del ciclo Sabathè risulta intermedio tra quello del ciclo Otto (più basso) e quello del ciclo Diesel (più alto). Nella pratica, i motori a ciclo Otto hanno rapporti di compressione più bassi — in genere tra $\epsilon \Ttildetilde 8 $ e 12 mentre nei motori Diesel o Sabathè questi valori sono più elevati, tra $\epsilon = 15$ e 23.

La ragione principale è che la benzina tende a detonare se troppo compressa, mentre nei motori a gasolio l’accensione spontanea è proprio l’effetto desiderato, e quindi si utilizzano compressioni più alte. Per questo motivo, anche se il rendimento teorico del ciclo Otto può sembrare buono, nella pratica i cicli Diesel e Sabathè raggiungono rendimenti effettivi più alti.

📝 In breve: Il ciclo Sabathè è un misto tra ciclo Otto e Diesel. Significa che durante la combustione, una parte del calore entra a volume costante come nel motore a benzina) e una parte a pressione costante (come nel motore a gasolio). Serve per rappresentare meglio i motori di media potenza. Alla fine, il rendimento è una via di mezzo tra Otto e Diesel, ma nella realtà può anche superare entrambi, perchè lavora con compressioni più alte senza problemi di detonazione.

Video spiegazione fatto da NotebookLM

Audio spiegazione fatto da NotebookLM

Reply by Email